Solving the Heat Equation (Dirichlet case) in 2 Dimensions using the Discrete Sine Transform

Contents

You first have to download m-files

Download the m-files sintr.m , isintr.m and put them in the same directory as your other m-files.

Solve the heat equation 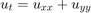$u_t=u_{xx} + u_{yy}$ in a rectangle

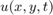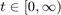The temperature in a rectangular plate is described by a function $u(x,y,t)$ for $x\in [0,A]$, $y\in[0,B]$, $t\in[0,\infty)$.

We assume that the temperature is zero on all four sides of the rectangle (Dirichlet conditions). The initial temperature 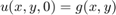$u(x,y,0)=g(x,y)$ is given.

The function 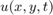$u(x,y,t)$ satisfies the heat equation:

$$u_t(x,y) = u_{xx}(x,y) + u_{yy}(x,y) \qquad x\in (0,A)$, $y\in(0,B) \quad\mbox{(PDE)}$$

We have Dirichlet boundary conditions on all four sides of the rectangle for all 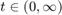$t\in(0,\infty)$:

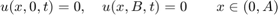
$$ u(x,0,t) = 0 , \quad u(x,B,t) = 0 \qquad x\in (0,A)$$

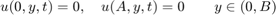
$$ u(0,y,t) = 0 , \quad u(A,y,t) = 0 \qquad y\in (0,B)$$

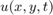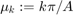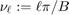
We write the solution $u(x,y,t)$ as a sine series with respect to both x and y: With $\mu_k:=k\pi/A$ and $\nu_\ell:=\ell\pi/B$

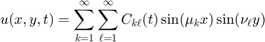
$$ u(x,y,t) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty C_{k\ell}(t) \sin(\mu_k x)\sin(\nu_\ell y)$$

From this we get 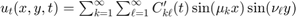$u_t(x,y,t) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty C_{k\ell}'(t) \sin(\mu_k x)\sin(\nu_\ell y)$ and

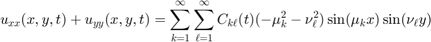
$$ u_{xx}(x,y,t) + u_{yy}(x,y,t) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty C_{k\ell}(t) (-\mu_k^2-\nu_\ell^2)\sin(\mu_k x)\sin(\nu_\ell y)$$

This gives the following Solution Formula: First find the sine series of 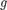$g$ with respect to both x and y:

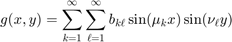
$$ g(x,y) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty b_{k\ell} \sin(\mu_k x)\sin(\nu_\ell y)$$

Then the solution is given by

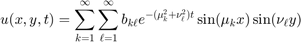
$$ u(x,y,t) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty b_{k\ell} e^{-(\mu_k^2+\nu_\ell^2)t} \sin(\mu_k x)\sin(\nu_\ell y)$$

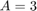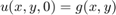Example: For a rectangle with lengths $A=3$ and $B=2$ we are given the initial condition $u(x,y,0)=g(x,y)$ with

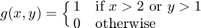
$$ g(x,y) = \cases{ 1 & if $x>2$ or $y>1$ \cr 0 & otherwise }$$

A=3; B=2;                       % lengths of rectangle sides
g = @(x,y) double((x>2)|(y>1)); % given function g(x,y) for initial condition

M = 100;                        % use spacing A/M for x
x = A*(1:M-1)/M;                % only interior nodes
N = 100;                        % use spacing B/N for y
y = B*(1:N-1)/N;                % only interior nodes

[X,Y] = ndgrid(x,y);            % X,Y are arrays of size M by N
G = g(X,Y);                     % G is array of values of g on grid:  G(j,k) = g(x_j,y_k)

surf(x,y,G');
xlabel('x'); ylabel('y'); title('given initial temperature')

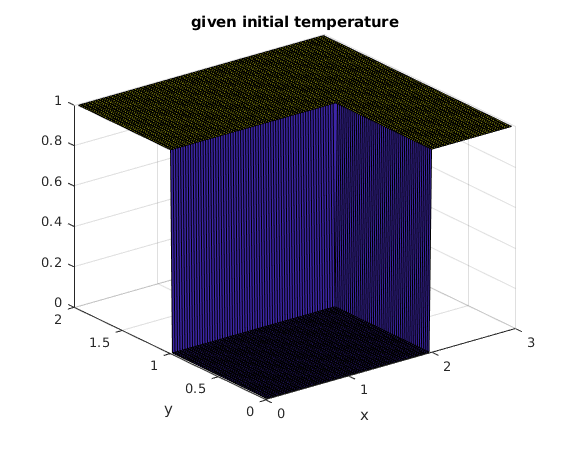
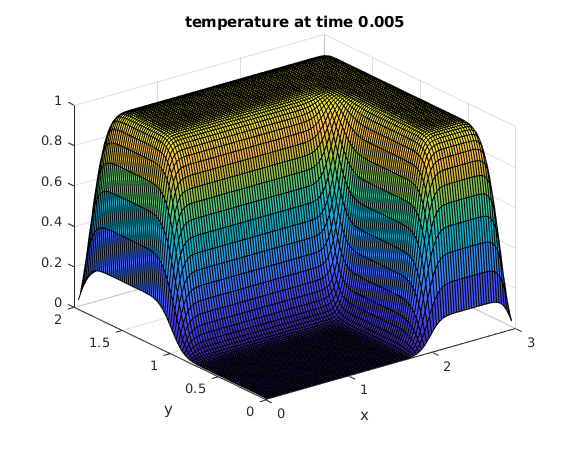
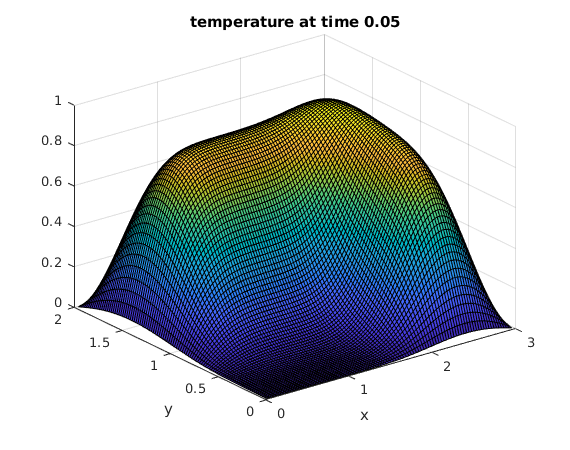
Use the discrete sine transform to compute the solution at several times

tv = [.005 .05];                % find solutions for these times

bx = sintr(G);                  % apply sine transform to columns
b = sintr(bx')';                % apply sine transform to rows

mu = (1:M-1)*pi/A;              % vector of mu_k
nu = (1:N-1)*pi/B;              % vector of nu_l
[Mu,Nu] = ndgrid(mu,nu);        % Mu,Nu are arrays of size M by N

for t=tv                        % for all times in vector tv
  C = b.*exp(-t*(Mu.^2+Nu.^2));   % solution formula in frequency domain
  Cx = isintr(C')';               % apply inverse sine transform to rows
  U = isintr(Cx);                 % apply inverse sine transform to columns
  surf(x,y,U');                   % make surface plot of solution
  xlabel('x'); ylabel('y'); title(sprintf('temperature at time %g',t))
  snapnow                         % show current figure
end


Published with MATLAB® R2018a