Solving an initial value problem for an ODE with the Laplace transform
Contents
Initial value problem:
Find the function y(t) which satisfies the differential equation
y'' + 2y' + y = g(t)
with the initial conditions
y(0) = 2, y'(0) = -3
and the right hand side function g(t) given by
g(t) = exp(3*t) for t<2
g(t) = 0 for t>=2
syms s t Y % define the symbolic variables
Find the Laplace transform of the right hand side function
If the right hand side function g(t) is defined as
g(t) = g1(t) for t<t0 g(t) = g2(t) for t>=t0
rewrite it as
g(t) = g1(t) + heaviside(t-t0)*(g2(t)-g1(t))
In our example we have t0=2, g1(t) = exp(3*t) and g2(t) = 0:
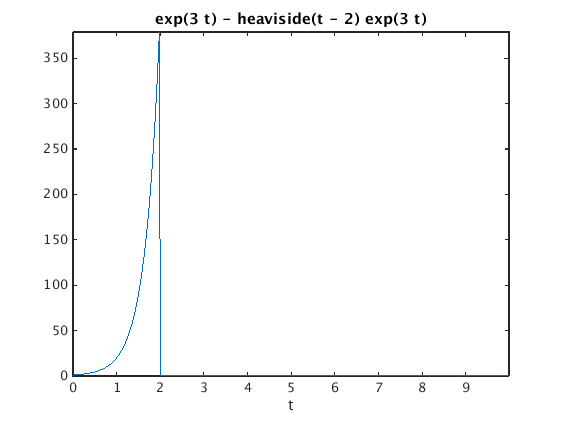
g = exp(3*t) - heaviside(t-2)*exp(3*t) ezplot(g,[0,10]); axis tight G = laplace(g,t,s) % find the Laplace transform of g(t)
g = exp(3*t) - heaviside(t - 2)*exp(3*t) G = 1/(s - 3) - (exp(-2*s)*exp(6))/(s - 3)
Apply the Laplace transform to the differential equation and solve for Y
Let Y1, Y2 denote the Laplace transforms of y', y'':
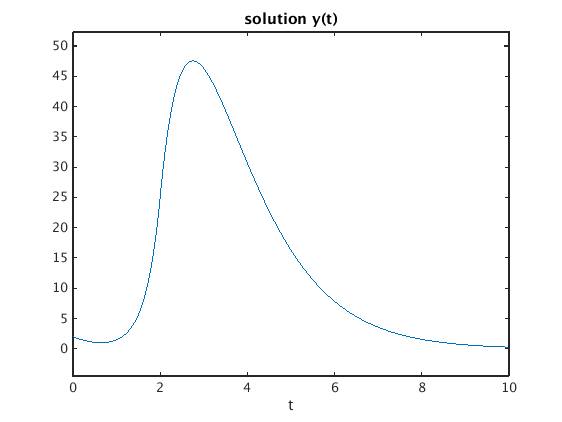
Y1 = s*Y - 2; % use initial condition y(0) = 2 Y2 = s*Y1 + 3; % use initial condition y'(0) = -3 Sol = solve(Y2 + 2*Y1 + Y - G, Y) % set lhs - rhs to zero and solve for Y sol = ilaplace(Sol,s,t) % apply inverse Laplace transform to get solution y(t) ezplot(sol,[0,10]) title('solution y(t)')
Sol = (2*s + 1/(s - 3) - (exp(-2*s)*exp(6))/(s - 3) + 1)/(s^2 + 2*s + 1) sol = (31*exp(-t))/16 + exp(3*t)/16 - (5*t*exp(-t))/4 + heaviside(t - 2)*exp(6)*(exp(2 - t)/16 - exp(3*t - 6)/16 + (exp(2 - t)*(t - 2))/4)