Solving a PDE using separation of variables

Contents

Problem

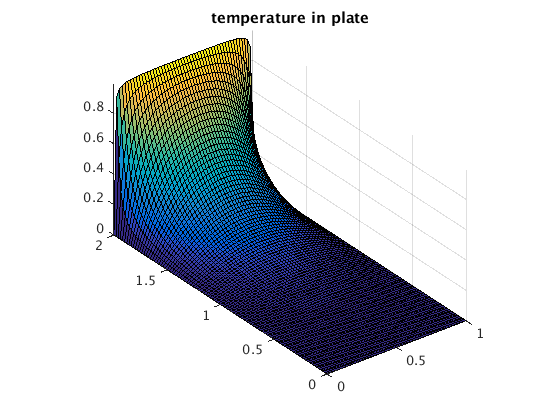
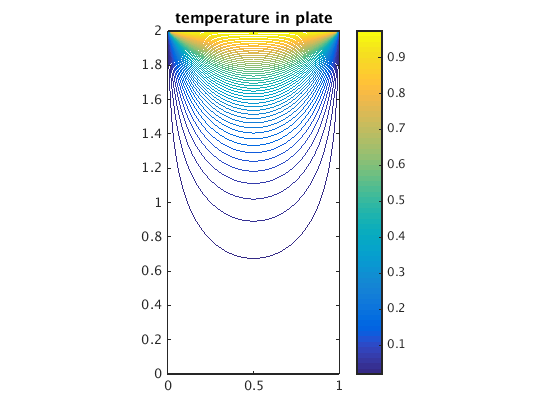
A rectangular plate 0<=x<=1 and 0<=y<=2 has temperature 0 on the bottom, left, and right edge. At the top edge the temperature is 1. Find the temperature u(x,y) in the plate!

In the rectangle 0<=x<=1 and 0<=y<=2 the function u(x,y) satisfies the PDE

u_{xx} + u_{yy}=0.

The boundary conditions are

Find the solution u(x,y)

Step 1: find solutions u(x,y)=v(x)w(y) with u=0 on the bottom, left, and right hand side.

Plugging this into the differential equation u_{xx}+u_{yy) = 0 and dividing by v(x)*w(y) gives

v''(x)/v(x) + w''(y)/w(y) = 0

Hence both terms have to be constant: v''(x)/v(x) = -lambda, w''(y)/w(y) = lambda

The first problem v''(x)/v(x) = -lambda has the solutions v(x) = A*cos(lambda^.5*x) + B*sin(lambda^.5*x) The condition v(0)=0 gives A = 0. The condition v(1)=0 gives sin(lambda^.5*x)=0 and hence lambda^.5 = k*pi. Hence we obtain the following nonzero solutions:

v(x) = sin(k*pi*x), k=1,2,... with lambda_k = k^2*pi^2, k=1,2,3,...

The second problem has the solutions

w(y) = A*exp(lambda^.5*y) + B*exp(-lambda^.5*y) = a*cosh(lambda^.5*y) + b*sinh(lambda^.5*y)

The condition w(0) = 0 gives a = 0. Hence we obtain

w(y) = b*sinh(k*pi*y)

yielding

u(x,y) = sum_{k=1,2,3...} u_k sin(k*pi*x) sinh(k*pi*y)

with some coefficients u_k which we still have to find.

Step 2: Find coefficients u_k using boundary condition on top side

Plugging in y=2 gives

u(x,2) = sum_{k=1,2,3...} u_k sinh(k*pi*2) sin(k*pi*x)

This is a sine series sum_{k=1,2,3,...} b_k sin(k*pi*x) We want u(x,2) = g(x) where g(x)=1 are the given boundary values on the top side.

Find the sine series for g(x)=1: b_k = 2*integral_{x=0...1} g(x)sin(k*pi*x) dx

Result: We obtain the sine series g(x) = 1 = sum_{k=1,3,5,...} 4/(k*pi) sin(k*pi*x)

Hence u_k = 4/(k*pi*sinh(k*pi*2)) for k=1,3,5,..., zero otherwise.

syms x k
Pi = sym('pi');

assume(k/2,'integer');                   % assume that k is even
b_even = simplify( 2*int(1*sin(k*Pi*x),x,0,1) )

assume((k+1)/2,'integer');               % assume that k is odd
b_odd = simplify( 2*int(1*sin(k*Pi*x),x,0,1) )

 
b_even =
 
0
 
 
b_odd =
 
4/(pi*k)
 

Resulting solution

We obtain

u(x,y) = sum_{k=1,3,5,...} 4/(k*pi*sinh(k*pi*2)) sin(k*pi*x) sinh(k*pi*y)

[X,Y] = meshgrid(0:.02:1,0:.02:2);       % grid for x and y values

U = zeros(size(X));
for k=1:2:100
  U = U + 4/(k*pi*sinh(k*pi*2))*sin(k*pi*X).*sinh(k*pi*Y);
end

figure(1); surf(X,Y,U); axis equal; title('temperature in plate')
figure(2); contour(X,Y,U,50); axis equal; colorbar; title('temperature in plate')

Published with MATLAB® R2014b