Solving the Wave Equation (Dirichlet case) in 2 Dimensions using the Discrete Sine Transform

Contents

You first have to download m-files

Download the m-files sintr.m , isintr.m and put them in the same directory as your other m-files.

Solve the wave equation $u_{tt}=u_{xx} + u_{yy}$ in a rectangle

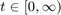We have a rectangular rubber membrane which is fixed at the boundary. The vertical displacement is described by a function $u(x,y,t)$ for $x\in [0,A]$, $y\in[0,B]$, $t\in[0,\infty)$.

We assume that the displacement is zero on all four sides of the rectangle (Dirichlet conditions). At time 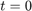$t=0$ the initial displacement 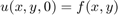$u(x,y,0)=f(x,y)$ and the initial velocity 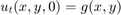$u_t(x,y,0)=g(x,y)$ is given.

The function 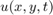$u(x,y,t)$ satisfies the wave equation:

$$u_{tt}(x,y) = u_{xx}(x,y) + u_{yy}(x,y) \qquad x\in (0,A)$, $y\in(0,B) \quad\mbox{(PDE)}$$

We have Dirichlet boundary conditions on all four sides of the rectangle for all 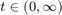$t\in(0,\infty)$:

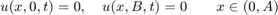
$$ u(x,0,t) = 0 , \quad u(x,B,t) = 0 \qquad x\in (0,A)$$

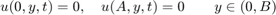
$$ u(0,y,t) = 0 , \quad u(A,y,t) = 0 \qquad y\in (0,B)$$

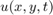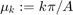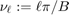
We write the solution $u(x,y,t)$ as a sine series with respect to both x and y: With $\mu_k:=k\pi/A$ and $\nu_\ell:=\ell\pi/B$

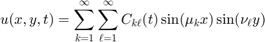
$$ u(x,y,t) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty C_{k\ell}(t) \sin(\mu_k x)\sin(\nu_\ell y)$$

From this we get 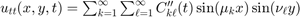$u_{tt}(x,y,t) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty C_{k\ell}''(t) \sin(\mu_k x)\sin(\nu_\ell y)$ and

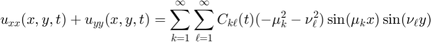
$$ u_{xx}(x,y,t) + u_{yy}(x,y,t) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty C_{k\ell}(t) (-\mu_k^2-\nu_\ell^2)\sin(\mu_k x)\sin(\nu_\ell y)$$

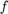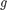This gives the following Solution Formula: First find the sine series of $f$ and $g$ with respect to both x and y:

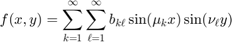
$$ f(x,y) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty b_{k\ell} \sin(\mu_k x)\sin(\nu_\ell y)$$

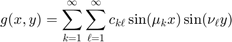
$$ g(x,y) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty c_{k\ell} \sin(\mu_k x)\sin(\nu_\ell y)$$

Let 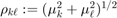$\rho_{k\ell}:=(\mu_k^2+\mu_\ell^2)^{1/2}$. Then the solution is given by

$$ u(x,y,t) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty \left[b_{k\ell} \cos(\rho_{k\ell}t) + \frac{c_{k\ell}}{\rho_{k\ell}}\sin(\rho_{k\ell}t) \right] \sin(\mu_k x)\sin(\nu_\ell y)$$

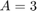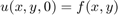Example: For a rectangle with lengths $A=3$ and $B=2$ we are given the initial conditions $u(x,y,0)=f(x,y)$ and $u_t(x,y,0)=0$ where

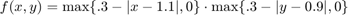
$$ f(x,y) = \max\{.3-|x-1.1|,0\}\cdot \max\{.3-|y-0.9|,0\}$$

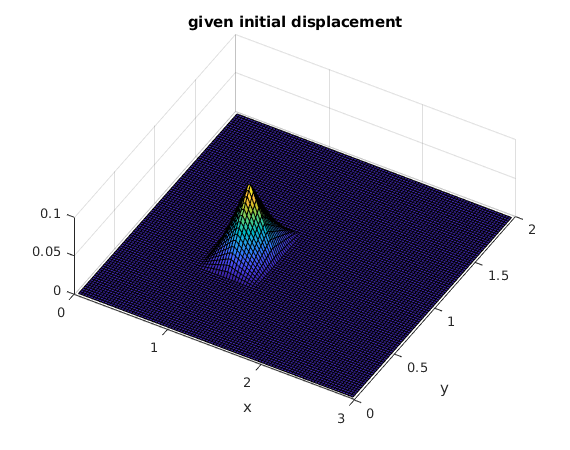
A=3; B=2;                       % lengths of rectangle sides
q = @(z) max(.3-abs(z),0);
f = @(x,y) q(x-1.1).*q(y-0.9);  % given function f(x,y) for initial condition

M = 100;                        % use spacing A/M for x
x = A*(1:M-1)/M;                % only interior nodes
N = 100;                        % use spacing B/N for y
y = B*(1:N-1)/N;                % only interior nodes

[X,Y] = ndgrid(x,y);            % X,Y are arrays of size M by N
F = f(X,Y);                     % F is array of values of f on grid:  F(j,k) = f(x_j,y_k)

surf(x,y,F');
view(30,70);
xlabel('x'); ylabel('y'); title('given initial displacement')

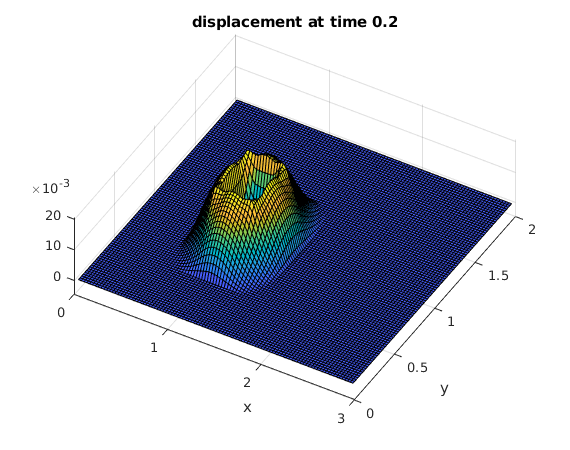
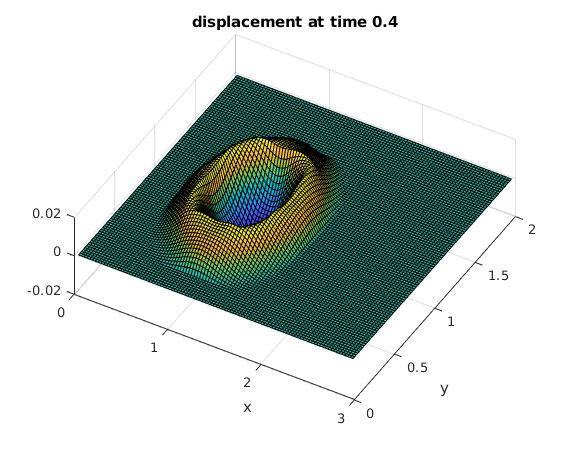
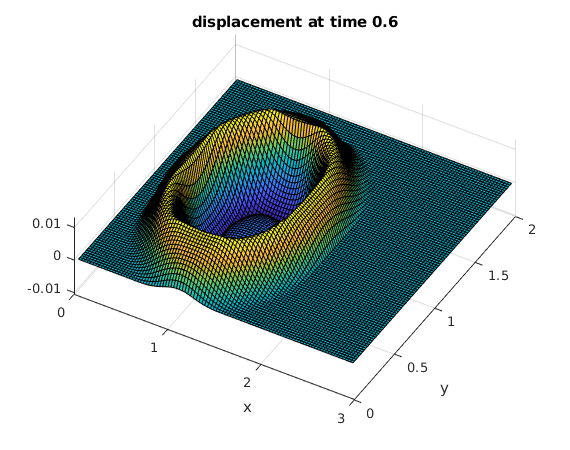
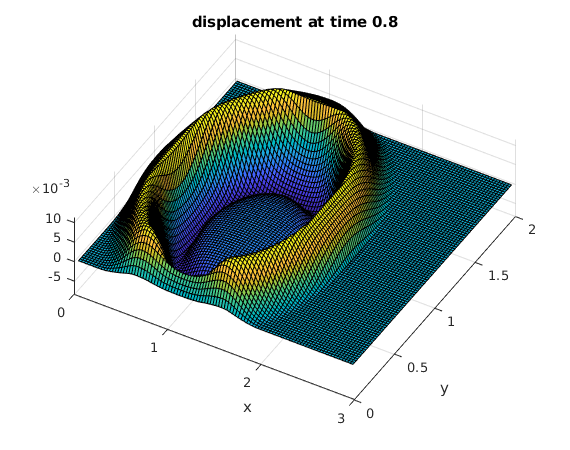
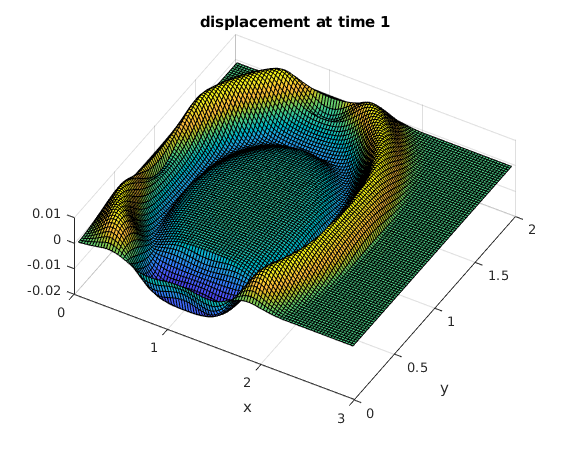
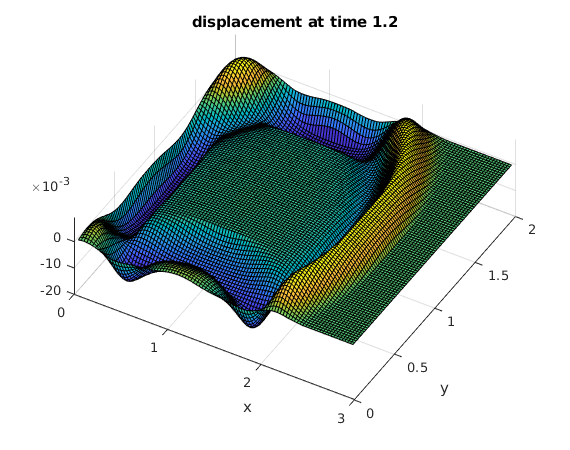
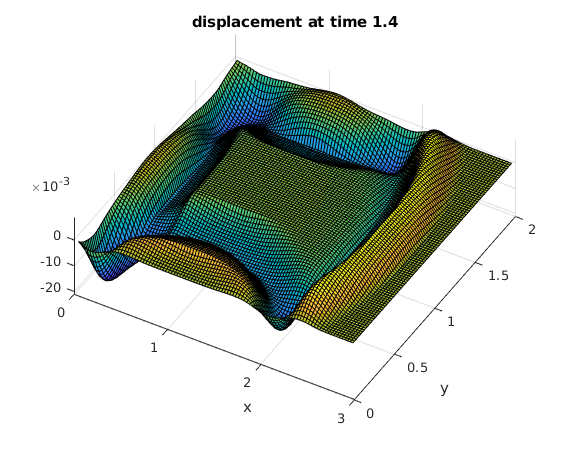
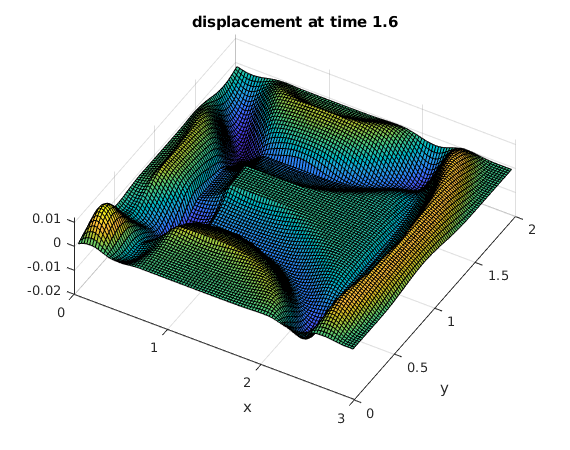
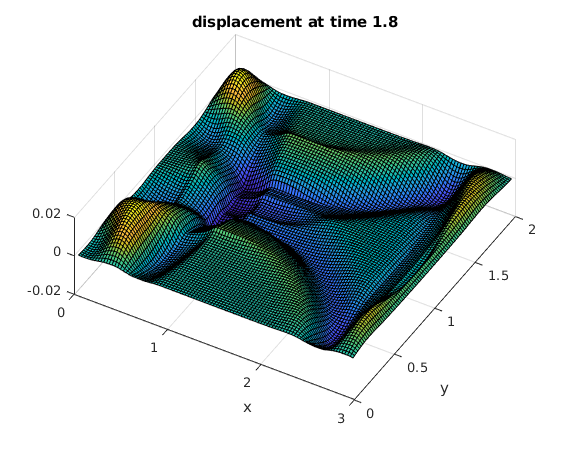
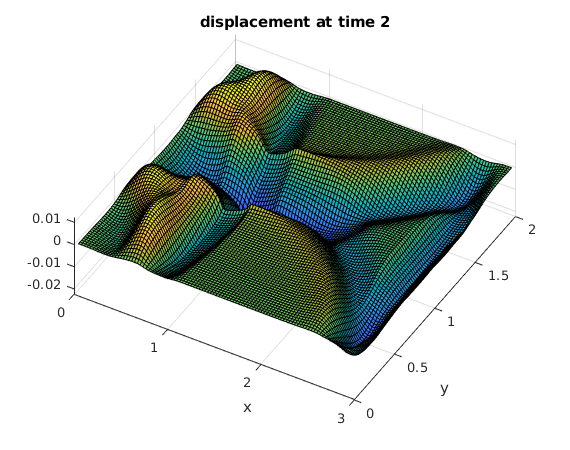
Use the discrete sine transform to compute the solution at several times

The initial peak causes an expanding circular wave. The waves are reflected at the four sides of the rectangle.

tv = .2:.2:2;                   % find solutions for these times

bx = sintr(F);                  % apply sine transform to columns
b = sintr(bx')';                % apply sine transform to rows

mu = (1:M-1)*pi/A;              % vector of mu_k
nu = (1:N-1)*pi/B;              % vector of nu_l
[Mu,Nu] = ndgrid(mu,nu);        % Mu,Nu are arrays of size M by N
rho = sqrt(Mu.^2+Nu.^2);        % rho from solution formula (array of size M by N)

for t=tv                        % for all times in vector tv
  C = b.*cos(rho*t);              % solution formula in frequency domain
  Cx = isintr(C')';               % apply inverse sine transform to rows
  U = isintr(Cx);                 % apply inverse sine transform to columns
  surf(x,y,U');                   % make surface plot of solution
  view(30,70);
  xlabel('x'); ylabel('y'); title(sprintf('displacement at time %g',t))
  snapnow                         % show current plot now
end


Published with MATLAB® R2018a