Nonlinear PDEs - Time-Dependent  No Title  Contents

References

Sc1

 L. Schwartz, MATHEMATICS FOR THE PHYSICAL SCIENCES, Hermann, 1966.

Elementary theory of distributions which he 'invented'.., Fourier transform (FT), and basic PDEs

Sc2

 L. Schawrtz, THÉORIE DES DISTRIBUTIONS, Hermann, 1966. The basic reference.

Ru

 W. Rudin, FUNCTIONAL ANALYSIS, Mcgraw-Hill, 1991.

Part II. on Distributions, FT and PDEs; given within the functional analysis formalism...

Fo1

 G. Folland, INTRODUCTION to PDEs, Princeton Univ. Press, 1976.

Graduate textbook; the basic trinity of PDEs in modern treatment; preliminaries with concise discussion on distributions, FT, etc...

Fo2

 G. Folland, REAL ANALYSIS. Modern Techniques and their Applications, Wiley, 1984.

§6 on stronf and weak 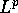 spaces; §8 on Fourier Transform convolutions distributions and Sobolev in a nut shell

Fr

 A. Friedman, PDEs of PARABOLIC TYPE, 1964.

Classical treatment of Parabolic equations; detailed proofs; consult also Friedman's 1969 PDEs and 1963 generalized functions

Ri

 R. Richtmyer, PRINCIPLES OF ADVANCED MATHEMATICAL PHYSICS, Springer-Verlag, 1978.

User friendly introductory textbook; §2-4 on Distributions and FT

GT

 D. Gilbarg & N. Trudinger ELLIPTIC PDEs of 2nd ORDER, Springer-Verlag, 1983.

Classical ref. for Elliptic PDEs; detailed Proofs; §7 contains a detailed discussion on Sobolev spaces

Hö

 L. Hörmander, THE ANALYSIS OF LINEAR PARTIAL DIFFERENTIAL OPERATORS, Vol. I, Springer-Verlag, 1983-1985.

Everything in an accesible discussion on distributions - Hörmander style,...

Tr

 F. Treves, BASIC LINEAR PDEs, 1975, Academic Press, The detailed theory on linear PDEs; readable discussion on Distributions, FT..

Ad

 R. Adams, SOBOLEV SPACES, Academic Press, 1975. A classical refrence with all the basics.

BTW

 P. Brenner, V. Thomee & L. Wahlbin, Besov Spaces and Applications for Difference Methods for Initial Value Problems, Lecture Notes in Mathematics, 434, Springer-Verlag, 1974.

Applications of Besov spaces to regularity of difference methods.

Ev

 C. Evans, PDEs, Berkeley Lecture Notes, 3A, 1993.

FJW

 M. Frazier, B. Jawerth & G. Weiss, Littlewood-Paley Theory and the Study of Function Spaces, A unified point of view

Tr

 H. Triebel, FUNCTIONS SPACES, Everything...

BS

 Bennett & Sharpley, INTERPOLATION OF OPERATOS, Academic Press, 1988.

A detailed account.

BL

 J. Bergh & J. Löfstrom, INTERPOLATION SPACES, An Introduction, Springer-Verlag, 1976.

DL

 R. DeVore & G. Lorntz, CONSTRUCTIVE APPROXIMATION, Springer-Verlag, 1993.

§2 on spaces of functions; §6 on K-functionlas and interpolation. Very readable

Fo2

 G. Folland, REAL ANALYSIS. Modern Techniques and their Applications, Wiley, 1984.

To

 A. Torchinsky, REAL VARIABLE METHODS in HARMONIC ANALYSIS, Academic Press, 1986. The Caderon-Zygmund 'program'; very readable.

St

 E. Stein, SINGULAR INTEGRALS AND DIFFERENTIABILITY OF FUNCTIONS, Princeton, 1970. The Classical redrence for the multi-variate case

Ta

 L. Tartar, Nonlinear PDEs Using Compactness Methods, Lecture Notes. Applications to Navier-Stokes and the nonlinear wave equations.