...perturbations
This is a rather strong notion of hyperbolicity; it restricts such hyperbolic system to be of first-order. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...:
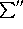tex2html_wrap_inline11155 (and respectively, tex2html_wrap_inline11157) indicate summation with tex2html_wrap_inline11159 of the first (and respectively, the first and the last) terms. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...points
We treat here the case of an odd number of 2N+1 collocation points. We get even in §2.2.3 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...with
348#288 correspond to Chebyshev family, 396#336 correspond to Legendre, etc. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...utilizing
Utilizing = integration by parts in this case. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...estimate
This should be compared with the straightforward 'familiar' bound 456#396. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
....
We note that in the previous constant coefficient case, the approximate model coincides with the differential case, hence the stability estimate was nothing but the a priori estimate for the differential equation itself. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...exponent,
To see this, use Duhammel's principle for 586#526 where 587#527 or integrate directly. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...sign
If a(x)>0, then (meth_ps.22) is semi-bounded (and hence stable) in the weighted 666#606-norm, with 667#607. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...reads
The last equality should be interpreted of course in the 697#637-sense, with tex2html_wrap_inline11109 limited by the initial 697#637-smoothness of 807#747. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...modes).
Either one can be carried out efficiently by the FFT. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...have
Here we utilize the fact that the error term in Gauss quadrature (2.5.4) is proportional to an intermediate value of the 2N-th derivative, 1024#964 (- e.g. consult (Gauss_Chebyshev.rule)) in the present context the inequality follows, 1025#965. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

Eitan Tadmor
Thu Jan 22 19:07:34 PST 1998