Initial Value Problems of Hyperbolic Type

0

The wave equation,
 
is the prototype for PDE's of hyperbolic type. We study the pure initial-value problem associated with (hyper.1), augmented with 2-periodic boundary conditions and subject to prescribed initial conditions,
 
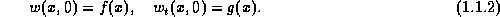
We can solve this equation using the method of characteristics, which yields
 
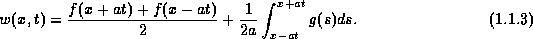
We shall study the manner in which the solution depends on the initial data. In this context the following features are of importance.  

1. : the principle of superposition holds.
2. : influence propagates with speed a. This is the essential feature of hyperbolicity. In the wave equation it is reflected by the fact that the value of w at (x,t) is not influenced by initial values outside domain of dependence (x - at, x + at).
3. for large enough set of admissible initial data: arbitrary initial data can be prescribed and the corresponding solution is .
4. : the solution is uniquely determined for by its initial data.
5. . The wave equation (hyper.1) describes the motion of a string with kinetic energy, , and potential one, . In order to show that the total energy
   
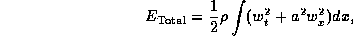
   is conserved in time we may proceed in one of two ways: either by the so called energy method or by Fourier analysis.

 
• The wave equation -- hyperbolicity by the energy method
• The wave equation -- hyperbolicity by Fourier analysis
• Hyperbolic systems with constant coefficients
• Hyperbolic systems with variable coefficients